이진트리
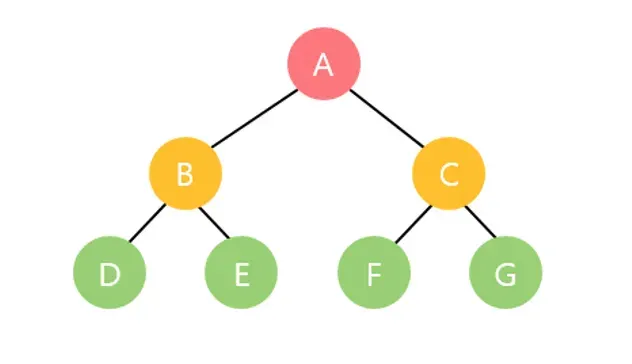
이진트리란 자식 노드가 최대 두 개인 노드들로 구성된 트리이다.
컴퓨터 과학에서 이진 탐색 트리(BST: binary search tree)는 다음과 같은 속성이 있는 이진 트리 자료 구조이다.
•
각 노드에 값이 있다.
•
값들은 전순서가 있다.
•
노드의 왼쪽 서브트리에는 그 노드의 값보다 작은 값들을 지닌 노드들로 이루어져 있다.
•
노드의 오른쪽 서브트리에는 그 노드의 값과 같거나 큰 값들을 지닌 노드들로 이루어져 있다.
•
좌우 하위 트리는 각각이 다시 이진 탐색 트리여야 한다.
포화 이진트리
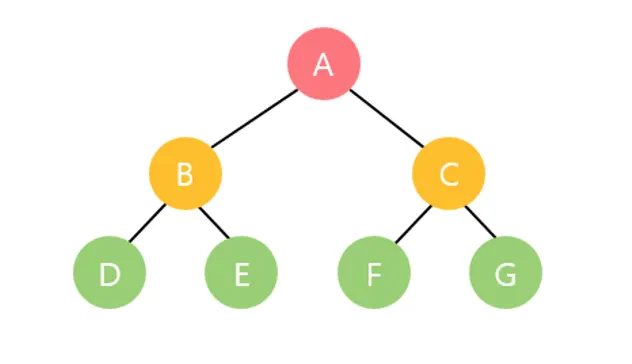
모든 노드가 두 개의 자식 노드를 가지며 모든 잎 노드가 동일한 레벨을 갖는다.
완전 이진트리
마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있으며, 마지막 레벨에서는 왼쪽부터 노드가
순서대로 채워져 있다.
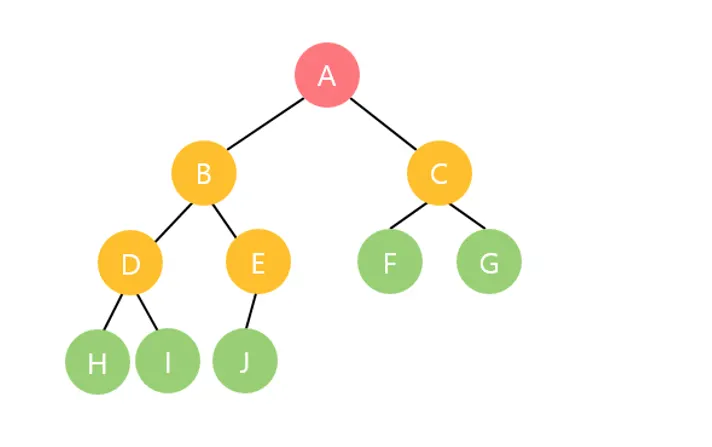
이진트리의 순회
전위 순회
루트 노드부터 잎 노드까지 아래 방향으로 순회
1.
자신 노드
2.
왼쪽 노드
3.
오른쪽 노드
중위 순회
왼쪽 하위 노드부터 오른쪽 하뤼 노드 방향으로 방문
1.
왼쪽 노드
2.
자신 노드
3.
오른쪽 노드
후진 순회
잎 노드를 모두 탐색하고 루트 노드를 방문
1.
왼쪽 노드
2.
오른쪽 노드
3.
자신 노드
이진 탐색 트리
탐색을 위한 이진트리
왼쪽 자식 노드는 자신보다 작고, 오른쪽 자식 노드는 자신보다 크다는 특징이 있다.
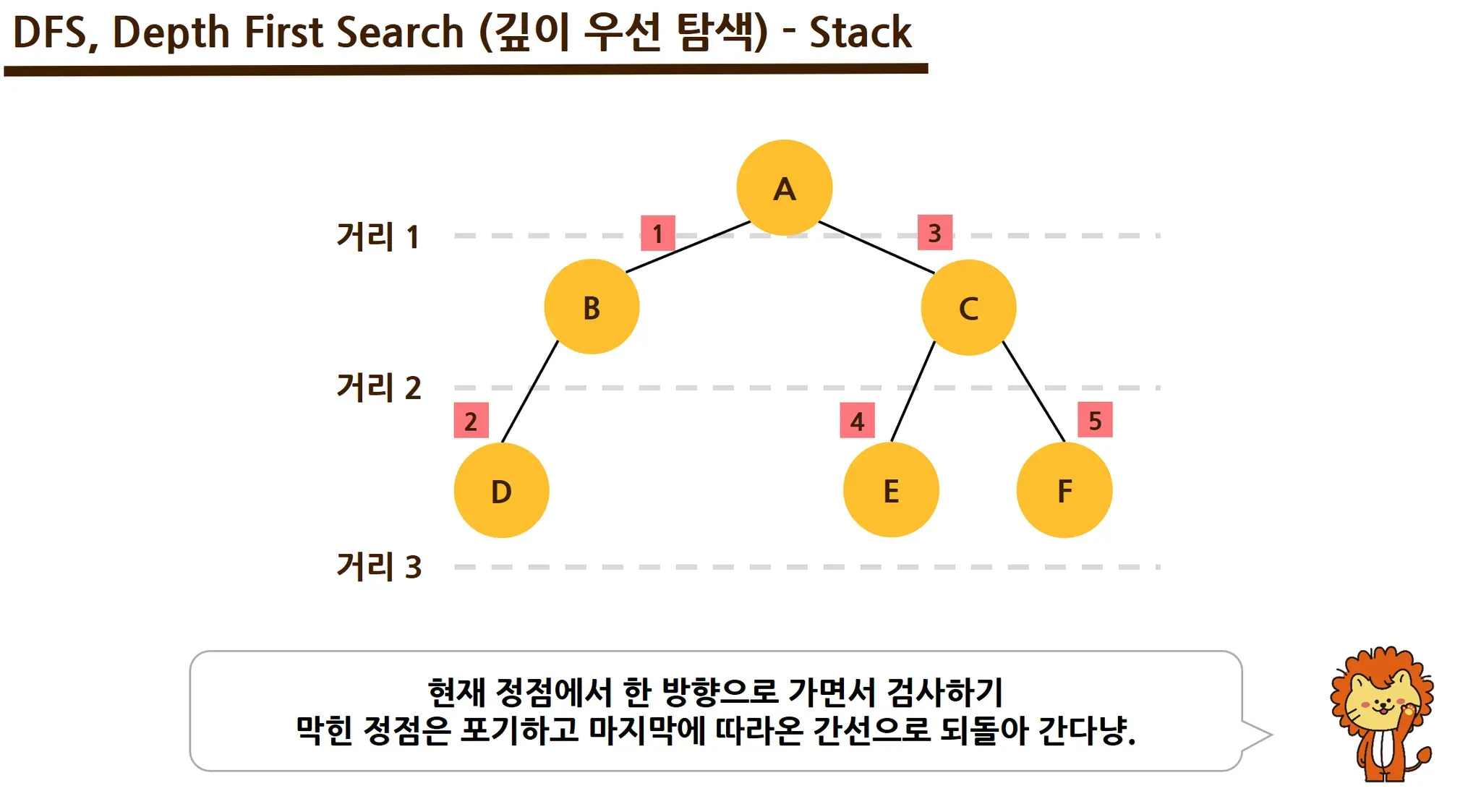
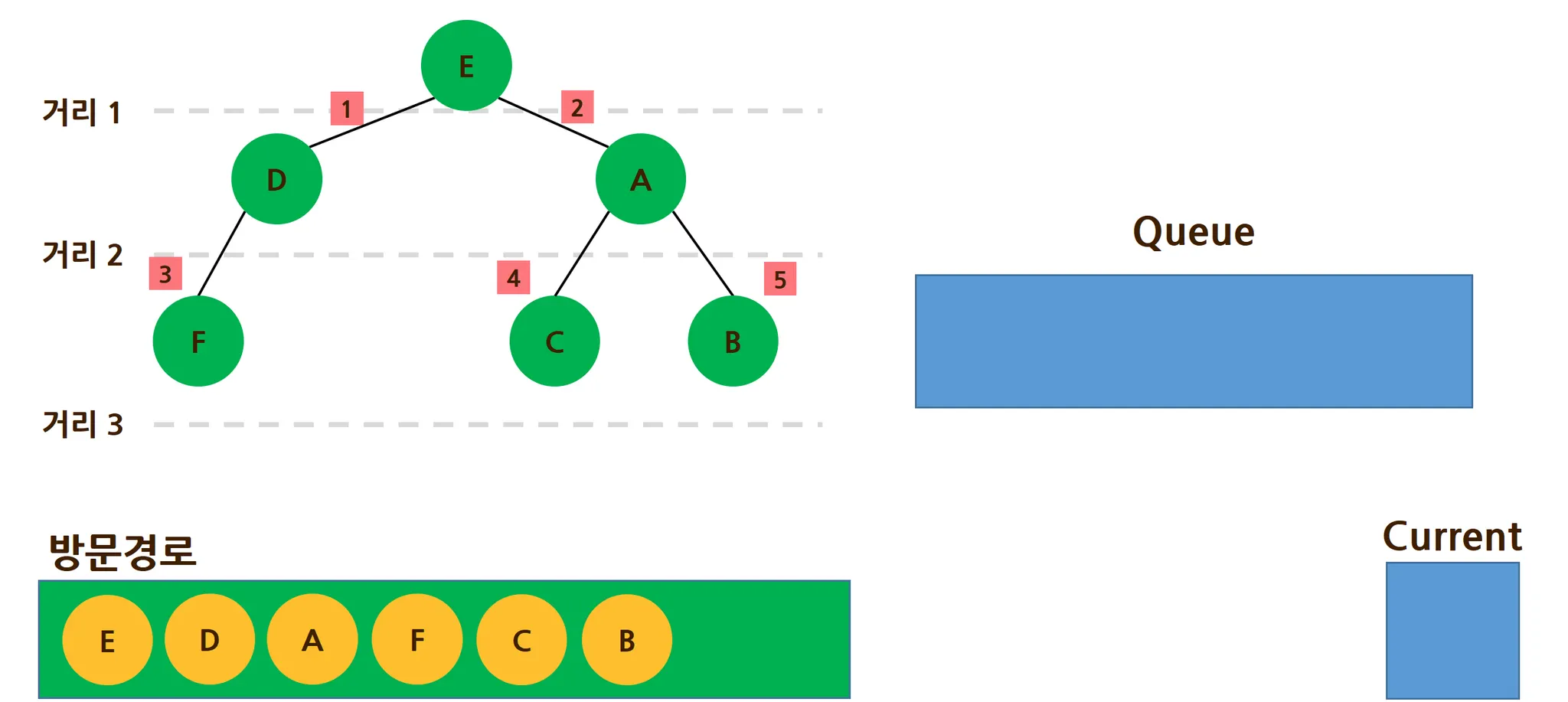
깊이 우선 탐색
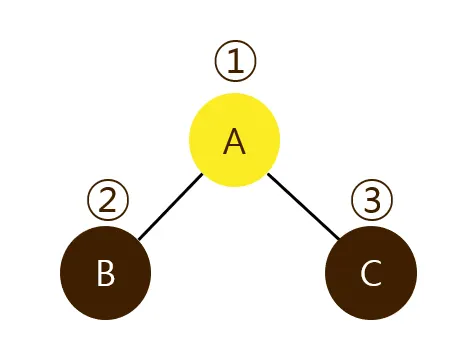
깊이 우선 탐색 (depth-first search: DFS)은 맹목적 탐색방법의 하나로 탐색트리의 최근에 첨가된 노드를 선택하고, 이 노드에 적용 가능한 동작자 중 하나를 적용하여 트리에 다음 수준(level)의 한 개의 자식노드를 첨가하며, 첨가된 자식 노드가 목표노드일 때까지 앞의 자식 노드의 첨가 과정을 반복해 가는 방식이다. (출처 :https://ko.wikipedia.org/wiki/깊이_우선_탐색)
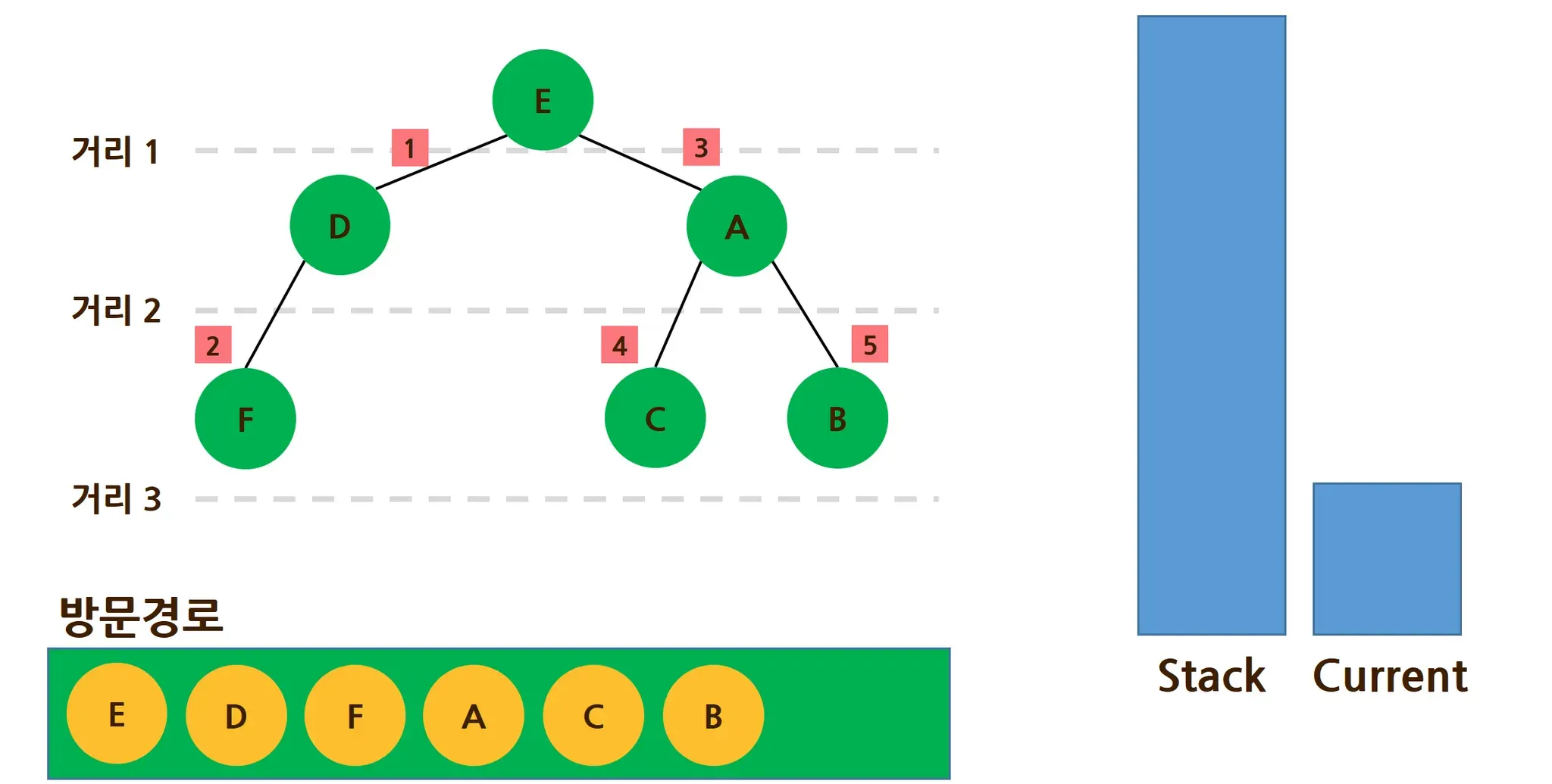
깊이 우선 탐색은 스택(stack)을 사용해서 탐색한다.
노란색 노드는 아직 방문하지 않은 노드, 초록색 노드는 방문한 노드이며, 스택에 담겨서 Current로, Current에서 방문경로로 이동하는 순간 그 노드와 연결되어 있던 노드들이 스택(Stack)으로 들어가게 된다.(문제 5번 설명 참고)노란색 노드는 아직 방문하지 않은 노드, 초록색 노드는 방문한 노드이며, 스택에 담겨서 Current로, Current에서 방문경로로 이동하는 순간 그 노드와 연결되어 있던 노드들이 큐(Queue)로 들어가게 된다.(문제 5번 설명 참고)
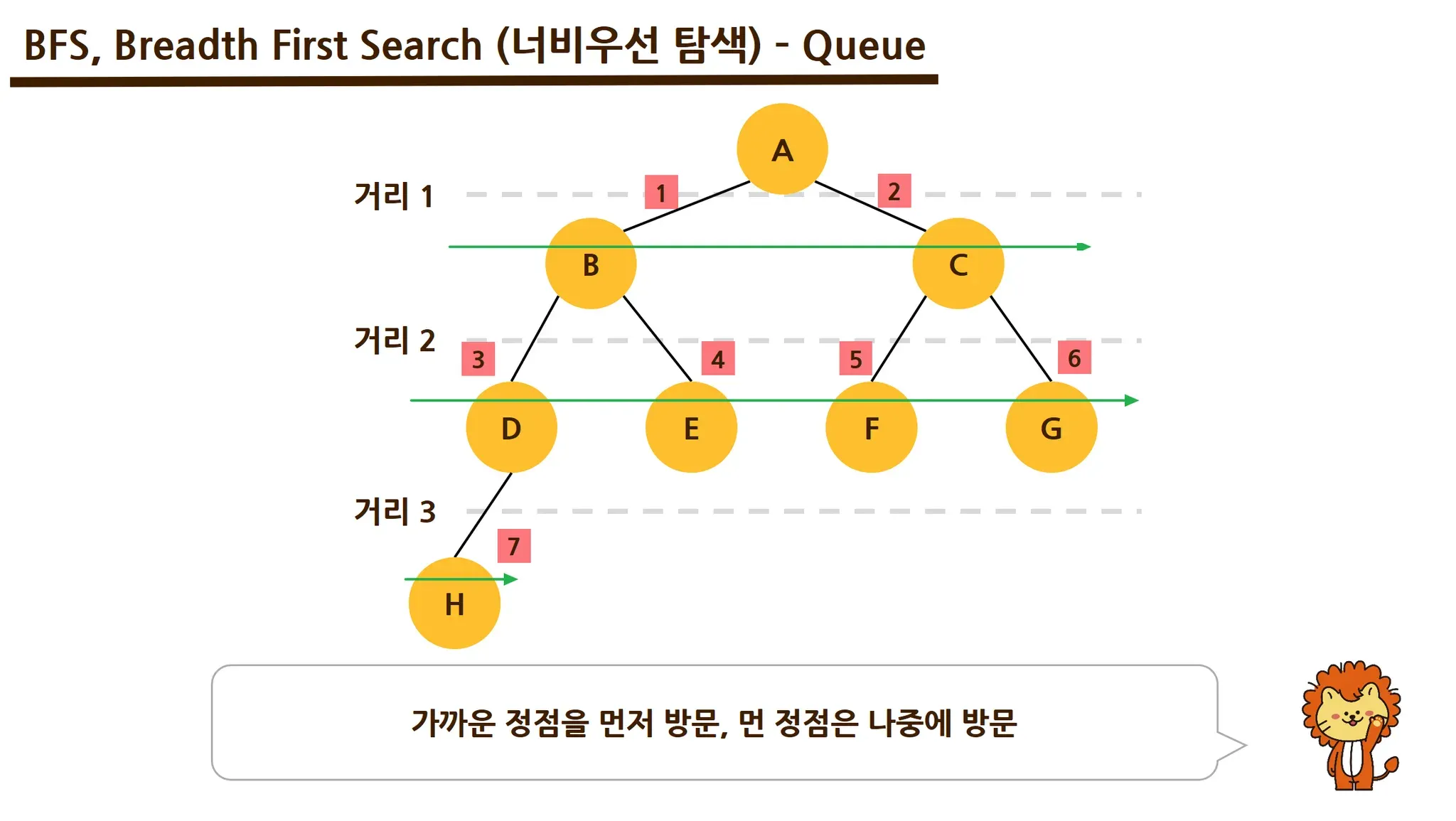
너비 우선 탐색
너비 우선 탐색(Breadth-first search, BFS)은 맹목적 탐색방법의 하나로 시작 정점을 방문한 후 시작 정점에 인접한 모든 정점들을 우선 방문하는 방법이다. 더 이상 방문하지 않은 정점이 없을 때까지 방문하지 않은 모든 정점들에 대해서도 너비 우선 검색을 적용한다. OPEN List 는 큐를 사용해야만 레벨 순서대로 접근이 가능하다. (출처 :https://ko.wikipedia.org/wiki/너비_우선_탐색)
노란색 노드는 아직 방문하지 않은 노드, 초록색 노드는 방문한 노드이며, 스택에 담겨서 Current로, Current에서 방문경로로 이동하는 순간 그 노드와 연결되어 있던 노드들이 큐(Queue)로 들어가게 된다.(문제 5번 설명 참고)
이진 탐색 트리에서의 검색
•
이진탐색트리에서 키 x를 가진 노드를 검색하고자 할때, 트리에 해당 노드가 존재하면 해당 노드를 리턴하고, 존재하지 않으면 NULL을 리턴한다.
•
검색하고자 하는 값을 루트노드와 먼저 비교하고, 일치할 경우 루트노드를 리턴한다.
◦
불일치하고 검색하고자 하는 값이 루트노드의 값보다 작을 경우 왼쪽 서브트리에서 재귀적으로 검색한다.
◦
불일치하고 검색하고자 하는 값이 루트노드의 값과 같거나 큰 경우 오른쪽 서브트리에서 재귀적으로 검색한다.
삽입
•
삽입을 하기 전, 검색을 수행한다.
•
트리를 검색한 후 키와 일치하는 노드가 없으면 마지막 노드에서 키와 노드의 크기를 비교하여서 왼쪽이나 오른쪽에 새로운 노드를 삽입한다.
function 삽입(data){
//노드 생성
const node = new Node(data, null, null);
//루트노드가 존재하지 않을 경우
if(this.root == null){
this.root = node;
} else {
let current = this.root;
let parent;
while(true){
parent = current;
if(data < current.data){
current = current.left;
if(current == null){
parent.left = node;
break;
}
} else {
current = current.right;
if(current == null){
parent.right = node;
break;
}
}
}
}
}
JavaScript
복사
삭제
삭제하려는 노드의 자식 수에 따라
•
자식노드가 없는 노드(리프 노드) 삭제 : 해당 노드를 단순히 삭제한다.
•
자식노드가 1개인 노드 삭제 : 해당 노드를 삭제하고 그 위치에 해당 노드의 자식노드를 대입한다.
•
자식노드가 2개인 노드 삭제 : 삭제하고자 하는 노드의 값을 해당 노드의 왼쪽 서브트리에서 가장 큰값으로 대체하거나, 오른쪽 서브트리에서 가장 작은 값으로 대체한 뒤, 해당 노드(왼쪽서브트리에서 가장 큰 값을 가지는 노드 또는 오른쪽 서브트리에서 가장 작은 값을 가지는 노드)를 삭제한다.
function del(node, data){
if(node == null){
return null;
}
if(data == node.data){
if(node.left == null && node.right == null){
return null;
}
if(node.left == null){
return node.right;
}
if(node.right == null){
return node.left;
}
//자식노드가 2개일 때
let tmp = this.delNode(node.right); //오른쪽 노드에서 가장 작은 값 가져오기
node.data = tmp.data;
node.right = this.del(node.right, tempNode.data);
return node;
}
else if(data < node.data){
node.left = this.del(node.left, data);
return node;
}
else{
node.right = this.del(node.right, data);
return node;
}
}
function delNode(node){
let temp2 = node;
while(tmp2.left !== null){
tmp2 = tmp2.left;
}
return tmp2;
}
JavaScript
복사
그 외
레드블랙트리
값이 루트 노드보다 작거나 큰 값만 들어올 경우 → 불균형한 이진탐색트리가 된다. 그러면 검색 효율이 저하된다.
이를 보완해 주는 것이 레드블랙트리 이다.
1.
트리의 모든 노드는 검정색과 빨간색이다
2.
루트 노드는 항상 검정색이다
3.
모든 잎 노드는 검정색 이다
4.
빨간색의 노드 자식들은 모두 검정색이지만, 검정색 노드 자식들은 검정색, 빨간색 모두 사용된다.
5.
루트 노드에서 모든 잎 노드 사이에 있는 검정색 노드의 수는 모두 동일하다.