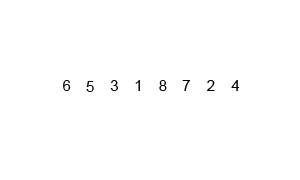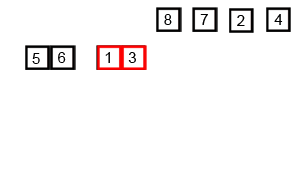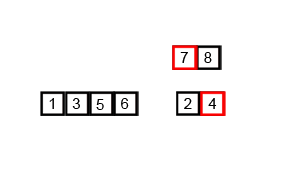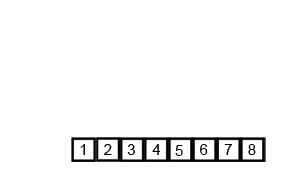정렬 알고리즘
•
원소들을 번호순이나 사전 순서와 같이 일정한 순서대로 열거하는 알고리즘이다. 효율적인 정렬은 탐색이나 병합 알고리즘처럼 (정렬된 리스트에서 바르게 동작하는) 다른 알고리즘을 최적화하는 데 중요하다.
정렬 알고리즘 종류
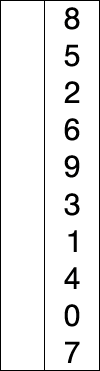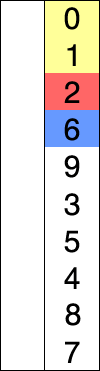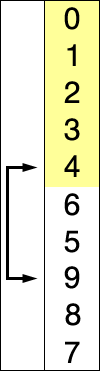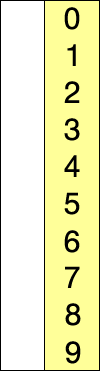
선택정렬
•
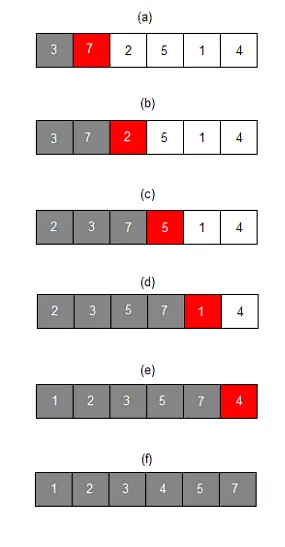
선택 정렬은 제자리 비교 정렬이다. 복잡도는 O(n2)이므로 큰 리스트에는 비효율적이며, 유사한 삽입 정렬보다 성능이 더 떨어지는 것이 일반적이다. 선택 정렬은 단순함이 특징이며 특정한 상황에서는 더 복잡한 알고리즘보다 성능상 우위가 있다.
•
이 알고리즘은 최소값을 찾고 값을 최초 위치와 바꿔친 다음 리스트의 나머지 부분에 대해 이 과정을 반복한다. 교환 과정은 n개를 넘지 않으므로 교환 비용이 많이 드는 상황에서 유용하다.
function selectionSort(arr) {
for (let i = 0; i < arr.length; i++) {
let min_index = i;
for (let j = i + 1; j < arr.length; j++) {
if (arr[min_index] > arr[j]) {
min_index = j;
}
}
let temp = arr[min_index];
arr[min_index] = arr[i];
arr[i] = temp;
}
return arr;
}
const arr = ['개구리', '거위', '말', '북극곰', '얼룩말', '고릴라', '기린', '닭', '코끼리'];
console.log(selectionSort(arr));
//['개구리', '거위', '고릴라', '기린', '닭', '말', '북극곰', '얼룩말', '코끼리']
JavaScript
복사
삽입정렬
•
삽입 정렬은 작은 리스트와 대부분 정렬된 리스트에 상대적으로 효율적인 단순한 정렬 알고리즘이며 더 복잡한 알고리즘의 일부분으로 사용되기도 한다.
•
리스트로부터 요소를 하나씩 취한 다음 마치 돈을 지갑에 넣는 방식과 비슷하게 이들을 올바른 위치에, 새로 정렬된 리스트에 삽입함으로써 동작한다. 배열의 경우 새 리스트와 남아있는 요소들은 배열 공간을 공유할 수 있으나 삽입의 경우 잇따르는 모든 요소를 하나씩 이동해야 하므로 비용이 많이 든다. 셸소트는 큰 리스트에 더 효율적인 삽입 정렬의 변종이다.
function insertIndex(sorted_arr, value) {
for(let i in sorted_arr){
if(value < sorted_arr[i]){
return i;
}
}
return sorted_arr.length;
}
function insertSort(arr) {
let sorted_arr = [];
while (arr.length != 0){
let value = arr.shift();
let index = insertIndex(sorted_arr, value);
sorted_arr.splice(index, 0, value);
}
return sorted_arr;
}
const arr = ['개구리', '거위', '말', '북극곰', '얼룩말', '고릴라', '기린', '닭', '코끼리'];
console.log(insertSort(arr));
//['개구리', '거위', '고릴라', '기린', '닭', '말', '북극곰', '얼룩말', '코끼리']
JavaScript
복사
병합정렬
•
합병 정렬 또는 병합 정렬(merge sort)은 O(n log n) 비교 기반 정렬 알고리즘이다.
1.
리스트의 길이가 1 이하이면 이미 정렬된 것으로 본다. 그렇지 않은 경우에는
2.
분할(divide) : 정렬되지 않은 리스트를 절반으로 잘라 비슷한 크기의 두 부분 리스트로 나눈다.
3.
4.
결합(combine) : 두 부분 리스트를 다시 하나의 정렬된 리스트로 합병한다. 이때 정렬 결과가 임시배열에 저장된다.
5.
복사(copy) : 임시 배열에 저장된 결과를 원래 배열에 복사한다.
function mergeSort(arr){
if (arr.length <= 1){
return arr;
}
const mid = Math.floor(arr.length / 2);
const left = arr.slice(0, mid);
const right = arr.slice(mid);
return merge(mergeSort(left), mergeSort(right));
}
function merge(left, right){
let result = [];
while (left.length && right.length){
if (left[0] < right[0]){
result.push(left.shift());
} else {
result.push(right.shift());
}
}
while (left.length) {
result.push(left.shift());
}
while (right.length) {
result.push(right.shift());
}
return result;
}
const arr = ['개구리', '거위', '말', '북극곰', '얼룩말', '고릴라', '기린', '닭', '코끼리'];
console.log(mergeSort(arr));
//['개구리', '거위', '고릴라', '기린', '닭', '말', '북극곰', '얼룩말', '코끼리']
JavaScript
복사
퀵정렬
•
퀵 정렬은 분할 정복(divide and conquer) 방법을 통해 리스트를 정렬한다.
1.
리스트 가운데서 하나의 원소를 고른다. 이렇게 고른 원소를 피벗이라고 한다.
2.
피벗 앞에는 피벗보다 값이 작은 모든 원소들이 오고, 피벗 뒤에는 피벗보다 값이 큰 모든 원소들이 오도록 피벗을 기준으로 리스트를 둘로 나눈다. 이렇게 리스트를 둘로 나누는 것을 분할이라고 한다. 분할을 마친 뒤에 피벗은 더 이상 움직이지 않는다.
3.
분할된 두 개의 작은 리스트에 대해 재귀(Recursion)적으로 이 과정을 반복한다. 재귀는 리스트의 크기가 0이나 1이 될 때까지 반복된다.
재귀 호출이 한번 진행될 때마다 최소한 하나의 원소는 최종적으로 위치가 정해지므로, 이 알고리즘은 반드시 끝난다는 것을 보장할 수 있다.
function quickSort(arr){
if (arr.length <= 1){
return arr;
}
const pivot = arr[0]; //기준점
const left = [];
const right = [];
for (let i=1; i<arr.length; i++){
if(arr[i] < pivot){
left.push(arr[i]);
} else {
right.push(arr[i]);
}
}
return quickSort(left).concat(pivot, quickSort(right));
}
const arr = ['개구리', '거위', '말', '북극곰', '얼룩말', '고릴라', '기린', '닭', '코끼리'];
console.log(quickSort(arr));
//['개구리', '거위', '고릴라', '기린', '닭', '말', '북극곰', '얼룩말', '코끼리']
JavaScript
복사